Origami: doblar papel no es solo entretenimiento

Los vínculos entre las matemáticas y el origami.
Hacer un avioncito o barquito de papel es algo común en la niñez. En esa etapa es un reto divertido, sin imaginar que esta práctica de doblar papel proviene de Japón.
En ese país hacer origami es una actividad de entretenimiento popular; muchos niños aprenden a hacer figuras de animales como grullas o ranas doblando hojas de papel.
El origami también es una técnica moderna de escultura en la cual pueden hacerse objetos extremadamente complejos solo doblando, sin cortar una hoja de papel.
Pero más allá del entretenimiento y el arte, esta práctica tiene detrás vínculos muy profundos con las matemáticas, afirma la doctora Julie Decaup, investigadora de la Unidad Cuernavaca del Instituto de Matemáticas de la UNAM.
De hecho, maestros lo utilizan para enseñar temas de matemáticas a sus estudiantes. El origami se relaciona con ramas de las matemáticas como geometría, álgebra y topología, entre otras.

Pliegues y despliegues.
Las figuras estéticas que se obtienen se basan en mapas de pliegues, explica la doctora.
Si desdoblas verás una figura de origami, el resultado es una hoja que tiene las marcas de los dobleces que se hicieron en el papel para lograr la figura tridimensional. A eso se le conoce como mapa de pliegues total.
Este mapa de pliegues incluye tanto los dobleces esenciales que al final forman el origami como los dobleces auxiliares, o aquellos que son necesarios para hacer los primeros.
Los mapas de pliegues orientados indican si el doblez es hacia arriba (montaña) o hacia abajo (valles). Los mapas de pliegues esenciales solamente muestran los pliegues del mismo nombre sin mostrar los pliegues auxiliares que también son necesarios.
A lo largo de los años, se ha desarrollado teoría matemática encargada de describir y formalizar los mapas de pliegues, los patrones geométricos y las reglas para crear las figuras de origami. Eso ha llevado a la creación de programas computacionales que permiten hacer automáticamente patrones de plegado.
Aplicaciones.
Comprender como plegar y desplegar eficientemente objetos tiene aplicaciones en la medicina, en el diseño de electrodomésticos y en ciencia espacial.
- Las bolsas de aire, que nos protegen en los automóviles, también son objetos que necesitan estar plegados en un espacio pequeño y activarse eficientemente cuando ocurre un accidente. Las matemáticas de origami permiten hacer simulaciones de su funcionamiento por computadora.
Otro ejemplo es un arreglo de paneles solares que se usó en un telescopio japonés puesto en órbita en 1995, el cual estaba plegado con técnicas de origami de forma que ocupara un espacio muy pequeño.
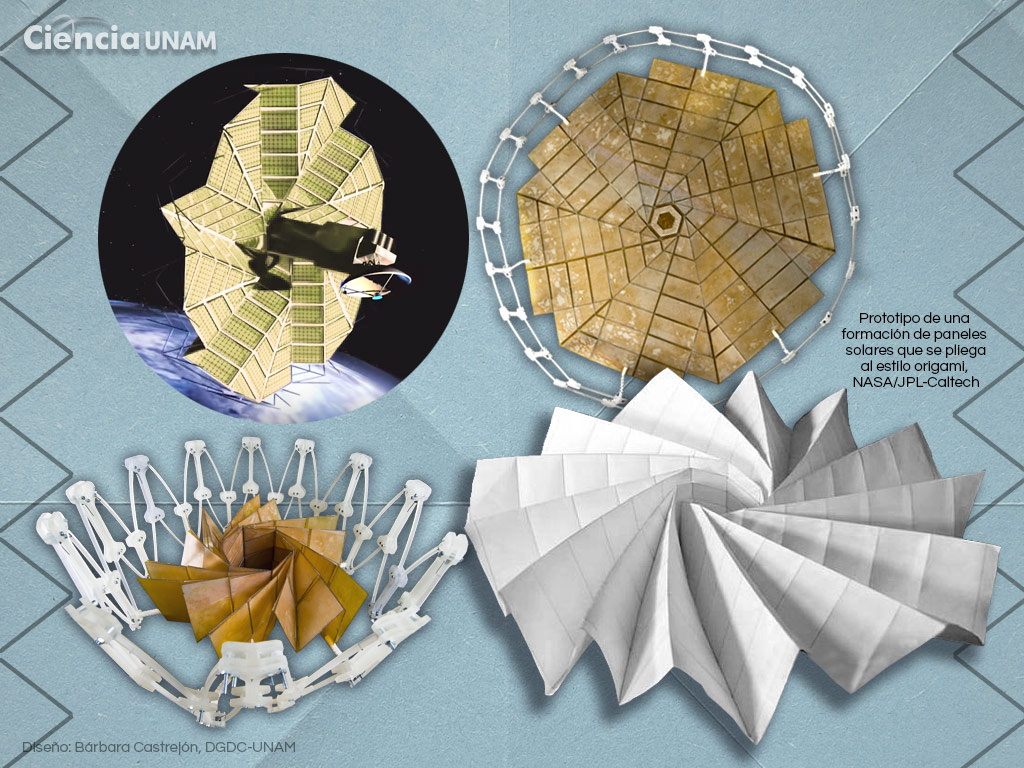
Otros telescopios que se encuentran en la fase de prototipo, como el Eyeglass Telescope, están empleando patrones de origami para plegar sus lentes en espacios reducidos y desplegarlos una vez que el telescopio se encuentre en el espacio.
Los stents son dispositivos que se colocan en el interior de un vaso sanguíneo o una arteria para mantenerlos abiertos y permitir que fluya la sangre. Deben introducirse, plegados de manera diminuta, a través de los vasos sanguíneos y desplegarse en el sitio donde son necesarios.
Científicos origamistas como Robert Lang y Zhong You han desarrollado stents que se pliegan siguiendo patrones de este arte de origen japonés.
Para saber más, te recomendamos:
Por: Naix’ieli Castillo.
Sitio Fuente: Ciencia UNAM
